TEORIA

HAMILTONIAN CEF i ODZIAŁYWAŃ MAGNETYCZNYCH
Potencjał kulombowski V w punkcie o współrzędnych (r, θ, φ) od­dalonym od początku układu współ­rzędnych o wektor r, jest wprost pro­por­cjonalny do sumy ładunków odda­lonych od początku układu współ­rzęd­nych o wektory R_i i od­wrotnie proporcjonalny do wartości odległo­ści pomię­dzy nimi i tym punktem:

gdzie sumowanie rozciąga się na wszystkie zewnętrzne ładunki punk­towe, bądź sferycznie-symetryczne. Określając α jako kąt po­między R i r można przedstawić iloraz po prawej stronie powyższego równania w postaci sumy funkcji Legen­dre’a:

Wyrażenie to jest prawdziwe dla r < R. Pomiędzy funkcjami Le­gendre’a a harmonikami sferycznymi istnieje  prosty związek:

Dzięki temu potencjał V(r, θ, φ) ła­dunków q_i można przedstawić w po­staci:

I analogicznie, w oparciu o tzw. harmoniki tesseralne zdefiniowane następująco:

Potencjał V można przedstawić jako:

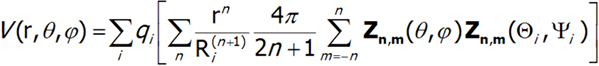
Dla dalszych rozważań wygodnie jest przyjąć znajomość rozkładu ładun­ków q_i i zastąpić wszystkie wielkości opisujące go jednym zbiorem  parametrów A^m_n:

Biorąc pod uwagę, że choć w ogólnej sytuacji współczynniki A^m_n mogą być zespolone, jednak waru­nki na rzeczywistość i hermitowskość potencjału V wymagają by:

Potencjał V można więc przedstawić w ogólnej  postaci:

Z powyższego szeregu multipolowego tylko niewielka liczba wyrazów jest nieze­rowa. Nieznikającymi elementami ma­cierzowymi potencjału V pomiędzy jednoelektronowymi stanami |l, l_z> i |l, l’_z> mogą być tylko te, które równo­cześnie spełniają dwa warunki:

1.  n ≤ 2l (warunek trójkąta dla całek harmonik sferycznych),   2.    l’- l ± m = 0

Z warunku trójkąta wynika, że w przy­padku elektronów d wartość n ≤ 4, natomiast dla rozważanych w niniejszej pracy elek­tronów f wartość n ≤ 6. Powyższe warunki po­zwalają określić liczbę niezerowych współczyn­ników opisujących potencjał elektro­statyczny. Biorąc pod uwagę elektrony d lub f, współczynników A^m_n mogą być zespolone, jednak waru­nki na rzeczywistość i hermitowskość potencjału V maksymalnie może być 27:

Istnienie środka symetrii otoczenia jonu centralnego pociąga za sobą redukcję współczynników o niepa­rzystej wartości n, jest to tzw. waru­nek parzystości. Rozważania symetrii oto­czenia prowadzą do wniosku, że obec­ność osi symetrii otoczenia redukuje ilość niezerowych współczynników . W przypadku osi 2-, 3-, 4-i 6-krotnej jest ich odpowiednio:15, 9, 7 i 5.   Znając symetrię otoczenia jonu paramagnetycznego, na podsta­wie znajomości harmonik tesseralnych można wyliczyć po­szczególne wyrazy rozwinięcia multipolowego potencjału V we współrzędnych karte­zjańskich. Jednoelektronowy hamilto­nian oddziaływania pola krystalicznego można więc ogólnie przedstawić w po­staci rozwinięcia multipolowego:

gdzie i numeruje elektrony niezamkniętej powłoki a ważniejsze podstawowe składowe rozwinięcia potencjału V(x,y,z) przyjmują znaną postać:

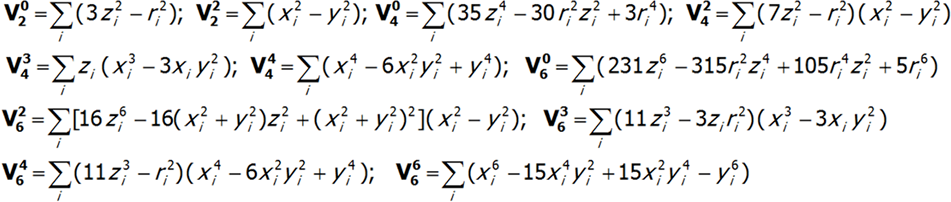
Kształt składowych multipolowych  potencjału V we współrzędnych karte­zjańskich jest zobrazowany na rys.2.4-7. Potencjały multipolowe  we współrzędnych kartezjańskich są jednorodnymi wielomianami stopnia n, można więc, z uwagi na związki komutacyjne operatorów L_x, L_y i L_z  kon­struować wyrażenia transformujące się identycznie jak one w oparciu o operatory J₊, J_ i J_z. Warto w tym miejscu przypomnieć, że:   L₊= L_x + iL_y i L_= L_x - iL_y oraz, że:  {L_+, L_}=2L_z, {L_z, L₊}= L_+, {L_z, L_{_}}= - L_.  Równoważna postać hamiltonianu konstruowana w oparciu o operatory Stevensa:  ,
różni się od postaci potencjałowej  współczynnikiem propor­cjonalności θ_n  i średnią wartością n-tej potęgi promienia niezamkniętej powłoki d lub f. Z uwagi na fakt, iż do opisu składowych potencjału używa się operatorów składo­wych całkowitego momentu pędu powłoki elektronowej stany własne ta­kiego hamiltonianu są stanami wieloelektronowymi. Hamiltonian wielo­elektronowy jonu z niezamkniętą powłoką f  w bazie stanów |J, J_Z> przyjmie postać:

 Ściśle zdefiniowany hamiltonian CEF, uzupełniony o sprzężenie spinowo-orbitalne, realizowany w pełnej bazie |L,S,Lz,Sz> jest postaci: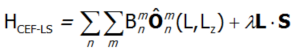.Dla porządku, pełny Hamiltonian uzupełniony o samouzgodnione oddziaływania magnetyczne ma postać: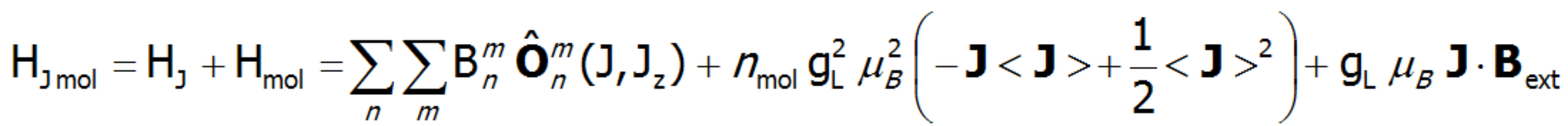

Zgodnie z nota­cją przyjętą notacją, skalujące współczyn­niki multiplika­tywne θ_n dla n = 2, 4 i 6 oznacza się pierwszymi greckimi li­terami, czyli: θ₂ = α, θ₄ = β, θ₆ = γ. Sposób obliczania współczynników skalu­jących potencjał w języku operatorów równoważnych dla stanów o tym sa­mym J został przedstawiony przez K.W.H Stevensa [2]. Wartości współczynników α, β i γ dla podstawowych multipletów jonów ziem rzad­kich zostały zebrane i ze­stawione w tabelach np. w pracach [3],[4]. Z drugiej strony powższe współczynniki dają się wyliczać analitycznie - stosowne procedury zostały zaimplementowane do aplikacji ATOMIC MATTERS.  Operatory Stevensa, w tym prztpadku rozpisane na składowe J-owe, w mają następujacą postać:

Znając elementy macierzowe operatorów J_z, J₊, J_ w bazie |J,J_z>:

można skonstruować macierz hamiltonianu uproszczonego, dla bazy |J,J_z>.

Znając, natomiast elementy macierzowe operatorów  elementy macierzowe operatorów L_z, S_z, L_x i S_x :

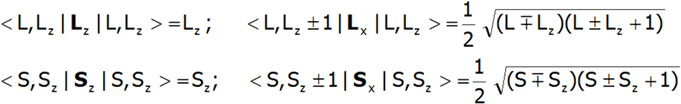
oraz elementy macierzowe operatora sprzężenia spin-orbita, , które nie są wyłącznie elementami diagonalnymi:

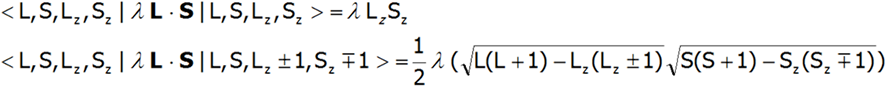
Tworzymy zatem pełny hamiltonian CEF dla bazy |L, L_z, S,S_z>, uzupełniony o samouzgodnione oddziaływania magnetyczne jest postaci:

Istnieje możliwość obliczenia wartości współczynników  w oparciu o wartości odległości koordynujących ligan­dów od jonu magnetycznego stosuje się tzw. model ładunków punktowych.

 Okazuje się, że pomimo uproszczenia (ligandy traktowane jako naładowane kule z jednorodnym powierzchniowym rozkładem ładunku, brak efektów ekranujących powłokę 4f przez powłoki 5s i 5p), model ładunków punkto­wych dla związków jonowych generuje strukturę stanów bliską obserwowanej doświadczalnie.

W przypadku związków międzymetalicznych model ładunków punktowych jest zbyt wielkim uprosz­czeniem. Z drugiej strony jednak w związkach międzymetalicznych powłoka 4f zachowuje swoją integralność a otoczenie sieciowe jonu paramagnetycz­nego ma zwykle dobrze określoną symetrię, stąd powyższe rozumowanie nakładające tylko warunki na symetrię otoczenia powłoki dalej jest poprawne, choć nie można już stosować bezpośredniej metody wyzna­czania parametrów , opartej tylko na znajomości odległości koordynują­cych jonów. W tej sytuacji wygodnie jest traktować iloczyn wielkości charakteryzujących wielkość wkładu poszczególnych multipoli, czyli: jako parametr pola krystalicznego . Tak sparame­tryzowany hamiltonian ma dobrze znaną postać:

Ilość niezerowych członów Stevensa w hamiltonianie CEF oczywiście zależy od symetrii otoczenia jonu paramagnetycznego w strukturze krystalicznej. W przypadku pola o symetrii rom­bowej, część hamiltonianu związana z oddziaływaniami polem elektryvcznym hamiltonian CEF zawiera następujące wyrazy:

dla otoczenia o strukturze heksagonalnej:

dla tetragonalnego otoczenia postać hamiltonianu CEF to:

pole kubiczne zaś opisuje się hamiltonianem:

Z uwagi na relacje pomiędzy parametrami kubicznego pola krystalicz­nego hamiltonian pola kubicznego (koordynacja tetraedrem, oktaedrem lub sześcianem) posiada tylko  dwa nie­zależne parametry i często przedstawia się go następująco

Strukturę stanów w polu kubicznym można przedstawia się czasem w postaci uproszczonej na tzw. diagramach LLW po sparametryzowaniu parametrów do B₄ i  B₆. Parametryzacja ta polega na wprowadzeniu dwóch nowych wielkości x i W [²⁷]. Celowość tej procedury polega na tym, że współczynnik x jest wówczas prawdziwą zmienną determinującą układ poziomów a czynnik W jedynie skaluje energię. Zależności pomiędzy parametrami B₄ i  B₆ oraz x i W są postaci:

F(4) i F(6) są wartościami stałymi dla danego pierwiastka i zależą od całkowitego momentu pędu J podstawowego multipletu.

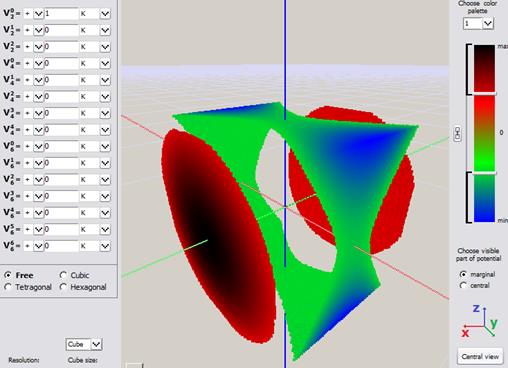
   a)

b)

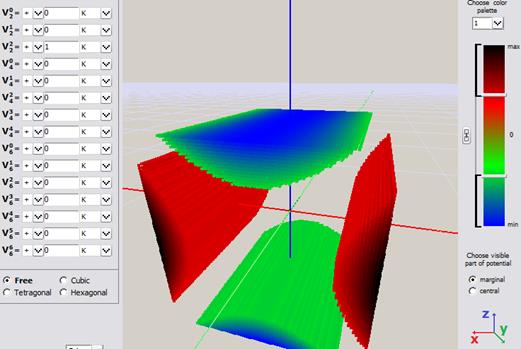
Rys. Przykładowe wizualizacje pochodzące z aplikacji ATOMIC MATTERS przedstawiające potencja­ł multipoli elektrostatycznych od­działują­cych na jon paramagnetyczny we  współrzędnych karte­zjańskich: a) Potencjał kwadrupola V⁰₂ b) Potencjał kwadrupola V²₂

Współczynnikami pola krystalicznego CEF są współczynniki A_n^m. Charakteryzują one rozkład ładunku w otoczeniu atomu/jonu poprzez określenie składowych rozwinięcia multipolowego potencjału zewnętrznego jonu/atomu. Innymi parametrami, za pomocą których można określić pole krystaliczne są tzw. parametry B_n^m . Dla tych parametrów hamiltonian trzeba tworzyć już nie w oparciu o potencjał V, a o operatory Stevensa i ich parametryzację. Aplikacja ATOMIC MATTERS pozwala zatem prowadzić obliczenia w oparciu o: lokalną symetrię otoczenia jonu paramagnetycznego, elektrostatyczne pole koordynujących ligandów (CEF) i wewnątrzjonowe oddziaływanie spinowo-orbitalne (s-o).
Z drugiej strony wykorzystując właściwości techniki operatorów równoważnych (twierdzenie Wignera-Eckarta) składowe multipolowe potencjału V zapisujemy równoważny hamiltonian  H_CEF  w zwięzłej postaci:

Co umożliwia wizualizację potencjału koordynującego, którą dostarcza aplikacja ATOMIC MATTERS w raz z kompletem wyników rachunkowych na zakładce wynikowej CEF Potentaial oraz testowo, w głównym oknie aplikacji, na zakładce POTENTIAL VISUALIZER. 

Rozwiązanie równania własnego Hamiltonianu pozwala uzyskać wartości energii (wartości własne) stanów elektronowych wraz z ich funkcjami falowymi w reprezentacji |L,S, J,J_z> oraz |L,L_z,S,S_z> w przypadku wszystkich jonów.

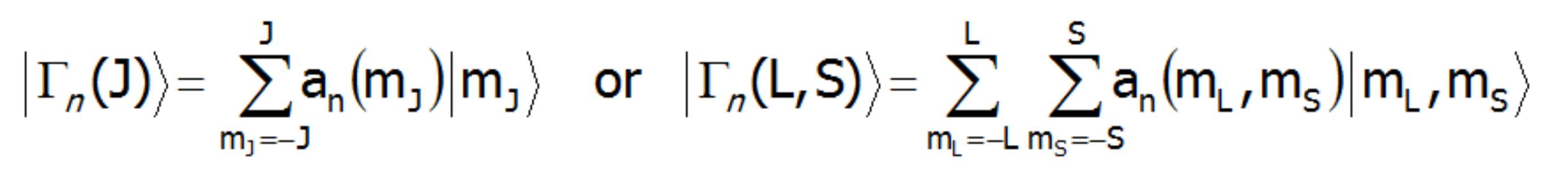
Warto pamiętać jednak, że wiarygodne rezultaty obliczeń w reprezentacji |J,J_z> są możliwe jedynie w przypadku jonów 4f, 5f . Reprezentacja |L S,L_z,S_z> jest adekwatna zawsze, w szczególności dla jonów/atomów z niezamkniętą powłoką p i d.

BIBLIOGRAFIA