TEORIA

ODDZIAŁYWANIA MAGNETYCZNE
Logicznym punktem startowym omówienia właściwości magnetycznych jonu w polu krystalicznym jest przedstawienie elementarnych właściwości silnie skorelowanych stanów wieloelektronowych niezamkniętej powłoki, co w efekcie sprowadza się do analizy wieloelektronowych funkcji falowych. Z powodu pewnych ciekawych konsekwencji, dobrze jest wcześniej wprowadzić podział jonów magnetycznych na takie, których niezamknięta powłoka zawiera nieparzystą liczbę elektronów – czyli na jony kramersowskie i takie gdzie liczba elektronów jest liczbą parzystą – jony niekramersowskie.  Takiego rozróżnienie jest spowodowane tym, że jedynie w przypadku jonów niekramersowskich pole krystaliczne o odpowiednio niskiej symetrii jest w stanie całkowicie znieść degenerację stanów multipletu. W przypadku jonu kramersowskiego pole krystaliczne o dowolnie niskiej symetrii nie może całkowicie znieść degeneracji, może jedynie rozszczepić multiplet tworząc co najwyżej dublety - tzw. dublety Kramersa. Obliczenia stanów pola krystalicznego CEF pozwalają uzyskać strukturę stanów, których funkcje własne są kombinacjami z-owych składowych całkowitego momentu pędu niezamkniętej powłoki. Baza funkcji własnych hamiltonianu pozwala znaleźć wartość oczekiwaną momentu magnetycznego każdego ze stanów w oparciu o znajomość funkcji falowej. Przy nieobecności pola magnetycznego stany multipletu częściowo rozszczepione polem krystalicznym nie posiadają momentu magnetycznego. W przypadku jonu kramersowskiego brak określonego momentu magnetycznego jest zawsze spowodowany przez pełną kompensację momentów magnetycznych zdegenerowanych stanów magnetycznych. Gdy jednak przyłożyć dowolnie małe zewnętrzne pole magnetyczne zostanie zniesiona degeneracja i pojawia się niezerowy moment magnetyczny rozszczepionych stanów. W przypadku jonów niekramersowskich, brak momentu magnetycznego stanów singletowych jest efektem samego kształtu funkcji falowej. Stany singletowe jonu niekramersowskiego zgodnie z elementarnym podejściem nie oddziałują z przyłożonym polem magnetycznym, jednak dokładna analiza w specyficznej sytuacji może prowadzić do przeciwnych wniosków. Dodatnia podatność magnetyczna atomów występuje jedynie wów­czas, gdy w atomie istnieje co najmniej jedna niedomknięta powłoka elektronowa. Według kwantowej teorii magnetyzmu na moment magne­tyczny układu elektro­nów składa się ich moment orbitalny oraz spinowy:

gdzie i oznacza sumowanie po elektronach oraz g_l =1, g_e =2.002324.

Dla atomów o określonym momencie pędu całej powłoki elektronowej J, moment magnetyczny tej powłoki jest proporcjonalny do J i przedstawia się wektorowym wyrażeniem:

Aby obliczyć wpływ zewnętrznego pola magnetycznego na jon paramagnetyczny (jedynie wówczas gdy J jest dobrą liczbą kwantową) znajdujący się w sieci należy dodać do hamiltonianu CEF człon Zeemanowski. Pamiętając, że zmiana energii stanu w polu magnetycznym δE = -m•B oraz, że:

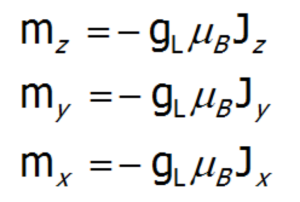
jednojonowy hamiltonian jonu w bazie |J,Jz>  w polu zewnętrznym przyjmie postać:

Analogicznie, dla bazy  |L, L_z, S,S_z>,pełny hamiltonian wraz z samouzgodnionymi oddziaływaniami magnetycznymi przybierze postać:

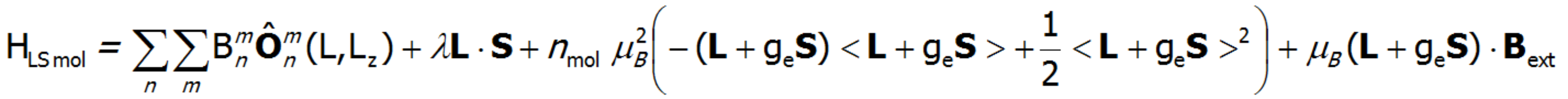
Wart podkreślenia jest fakt, iż w zależności od kierunku przyłożonego pola zewnętrznego, w ogólnym przypadku otrzymuje się zróżnicowane właściwości magnetyczne jonu z uwagi na symetrię otoczenia względem lokalnych osi współrzędnych. Aby więc obliczyć wpływ różnych składowych kierunkowych pola zewnętrznego w miejsce symbolicznie zapisanego J•B_zew w hamiltonianie realizowanym w bazie |J,J_z> oblicza się osobno: J_ZB_z, J_xB_x i J_YB_y. Istotne dla całości rozważań jest podkreślenie, że zarówno człon hamiltonianu - CEF jak i zeemanowski diagonalizowane są jako całość (równocześnie), co w efekcie ustala oddziaływania pomiędzy poszczególnymi stanami CEF w niezerowych polach magnetycznych. Całość dotychczasowych rozważań dotyczyła właściwości magnetycznych nieoddziałujących między sobą jonów paramagnetycznych. Przedstawiane podejście uwzględnia jednak magnetyczne oddziaływania wymienne pomiędzy jonami paramagnetycznymi. Podstawowa idea tych obliczeń opiera się na przybliżeniu pola molekularnego. Dla uproszczenia rozważań rachunków dla pola molekularnego przedstawiaono dla „wąskiej bazy” |J,J_z> (Rozumowanie dla pełnej bzay |L,L_z,S,S_z> jest analogiczne). Jeśli w członie zeemanowskim hamiltonianu zastąpić zewnętrzne pole wewnętrznym polem molekularnym pochodzącym od magnetycznych identycznych sąsiadów w sieci, to można je będzie przedstawić jako:

gdzie <J> oznacza średnią temperaturową wektora całkowitego momentu pędu powłoki. Współczynnik pola molekularnego n_mol opisuje ilościowo stosunek wartości pola molekularnego w miejscu jonu magnetycznego do momentu magnetycznego jonu będącego jego źródłem. Z uwagi na to, że żaden z jonów paramagnetycznych w sieci krystalicznej nie jest wyróżniony, wszystkie muszą oddziaływać ze sobą w identyczny sposób. Zmiana energii i-tego stanu jonu paramagnetycznego w polu magnetycznym pochodzącym od jonów zewnętrznych jest więc równa:

gdzie J_i jest wektorem momentu pędu związanym z każdym stanem CEF. Tak zdefiniowane pole molekularne umożliwia konstrukcję hamiltonianu zawierającego oddziaływania samouzgadniające się. Jon paramagnetyczny jest źródłem pola magnetycznego, ponieważ zostaje na nim indukowany moment magnetyczny, którego przyczyną są pola magnetyczne pochodzące od innych jonów z indukowanym momentem przez następne jony itd. Konstruując samouzgodniony hamiltonian jonu 4f należy uważać by nie obliczać energii układu jonów magnetycznych jako sumy energii poszczególnych jonów. Należy bowiem pamiętać o tym, że choć wszystkie stany zmieniają swoją energię, to część energii jest związana z samym polem (analogicznie jak energia kondensatora czy magnetyczna energia cewki z prądem). Całkowitą energię układu jonów określa więc energia poszczególnych jonów w polu molekularnym pomniejszona o energię wytworzonego przez nie pola [[6]]:

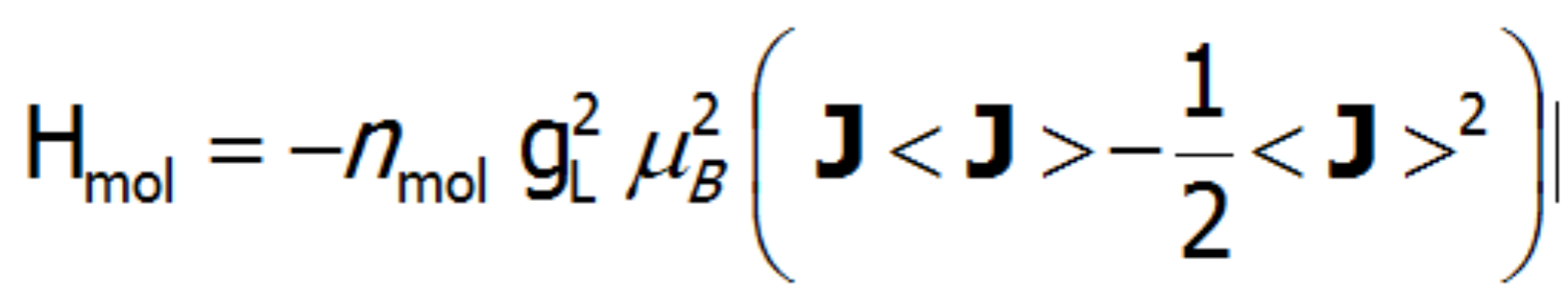
Mając zdefiniowane człony hamiltonianu opisujące oddziaływanie układu wieloelektronowego z polem krystalicznym, magnetyczne oddziaływanie wymienne oraz oddziaływanie z zewnętrznym polem magnetycznym można wreszcie przedstawić postać całego hamiltonianu realizowanego w bazie |J,J_z> :

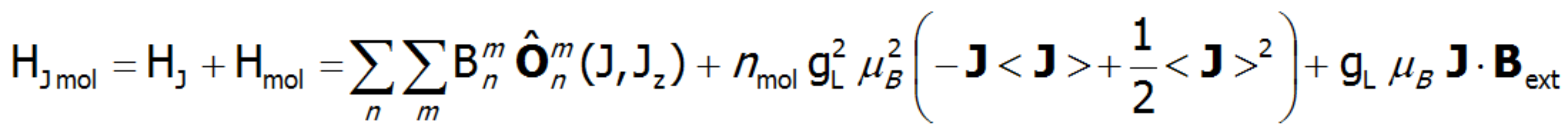
Zawiera on zarówno człony jednojonowe jak i międzyjonowe pozwalając w przypadku obliczeń numerycznych, dla każdego kroku temperaturowego na jednoczesną diagonalizację wszystkich członów. Umożliwia to określenie energii własnych i kierunkowych składowych całkowitego momentu pędu niezamkniętej powłoki dla poszczególnych stanów własnych Γ_i, obliczanych jako kwadraty funkcji falowych w reprezentacji krętowej. W praktyce rozwiązanie równania własnego hamiltonianu opisanego typu sprowadza się do diagonalizacji macierzy (2J+1)·(2J+1), co oczywiście prowadzi do uzyskania wartości energii 2J+1 stanów. Biorąc pod uwagę, że:

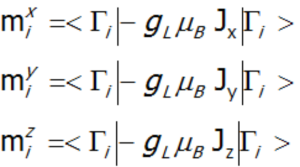
z każdym (i-tym) stanem struktury subtelnej można wiązać jego moment magnetyczny (gdzie: g_L – czynnik Landego).

MOMENT MAGNETYCZNY I NAMAGNESOWANIE
Obliczanie namagnesowania, w przyjętej metodologii, sprowadza się do sumowania identycznie zachowujących się momentów magnetycznych poszczególnych jonów z niezamkniętą powłoką elektronową. Z uwagi na to, że jony ziem rzadkich znajdują się w samouzgodnionym polu molekularnym, wartość ich momentu magnetycznego zmienia się z temperaturą. Pamiętając, że z każdym stanem własnym hamiltonianu CEF związany jest jego moment magnetyczny, całkowity moment silnie skorelowanego układu elektronowego w danej temperaturze jest wypadkowym momentem z obsadzonych stanów obliczonym z wagą boltzmannowską:

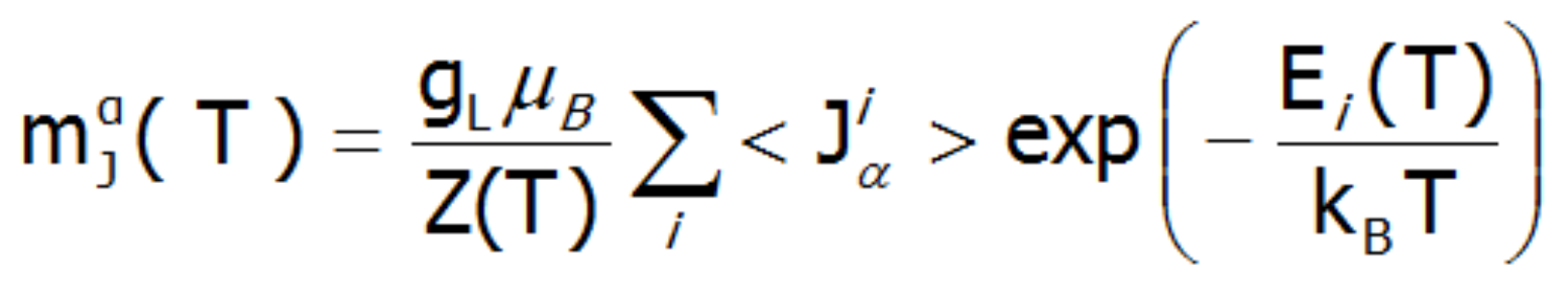
W powyższym równaniu indeks α – oznacza składową kierunkową, i – numeruje stany własne hamiltonianu, natomiast <Jⁱ_α > oznacza wartość oczekiwana rzutu całkowitego krętu całej powłoki na oś α  w i-tym stanie. Warto w tym miejscu podkreślić, że w T = 0 gdy obsadzony jest jedynie stan podstawowy, namagnesowanie układu jonów 4f w przeliczeniu na 1 jon jest równe wartości oczekiwanej momentu magnetycznego stanu podstawowego. Z uwagi na to, że w przyjętym modelu wszystkie jony zachowują się identycznie obliczona zależność temperaturowa momentu magnetycznego jest ściśle związana z wartością pola molekularnego, która wynosi:

Wartość współczynnika pola molekularnego n_mol określa temperaturę pojawiania się porządku magnetycznego T_c. Obliczenia namagnesowania w stanie uporządkowanym pozwalają wyznaczyć anizotropię magnetokrystaliczną układu. W przypadku symetrii tetragonalnej rozwinięcie energii anizotropii można przedstawić w znanej postaci:

gdzie K_i(T) są zależnymi od temperatury współczynnikami anizotropii, a θ i φ biegunowymi kątami opisującymi kierunek momentu magnetycznego względem wzajemnie prostopadłych osi krystalograficznych. Współczynniki K_i(T) są w ścisłym związku z parametrami pola krystalicznego. W polu o symetrii tetragonalnej mają one wartość:

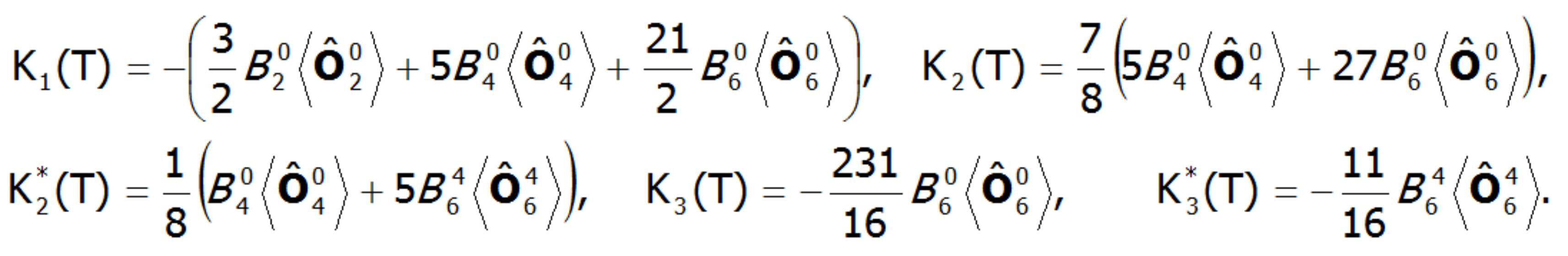
gdzie  oznacza średnie temperaturowe operatorów Stevensa. Możliwość obliczania wartości indukowanych momentów magnetycznych w polu zewnętrznym przyłożonym w różnych kierunkach pozwala na bezpośrednie określenie anizotropii magnetokrystalicznej. Przedstawione podejście pozwala w klarowny sposób określić składowe całkowitego momentu magnetycznego jonów paramagnetycznych. Całkowity moment magnetyczny jonu składa się z części orbitalnej i spinowej: m_c=m_L+m_S. Znajomość wartości oczekiwanych składowych wektora momentu pędu poszczególnych stanów <Jⁱ_α > pozwala określić udział części spinowej i orbitalnej momentu magnetycznego. Pamiętając, że:

oraz biorąc pod uwagę, że g_l = 1 i g_s = 2.002324:

dostaje się:

Z powyższych związków wynika, że stosunki poszczególnych składowych momentu magnetycznego do momentu całkowitego są stałe dla danego jonu i niezależnie od otoczenia i temperatury: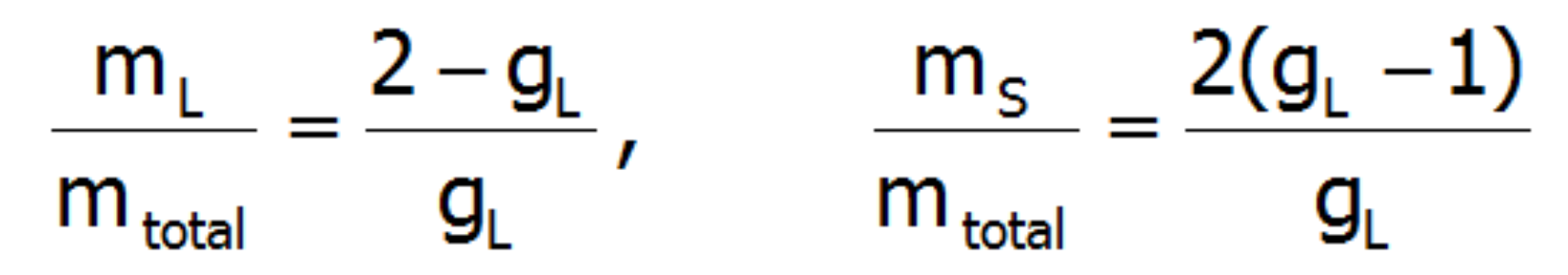

Zagadnienie dokładności powyższego rozumowania jest omówione na początku opisu podstaw teoretycznych aplikacji przy okazji porównania wyników obliczeń wykonywanych w bazie |J,J_z> w stosunku do obliczeń prowadzonych dla bazy pełniejszej |L,S,L_z,S_z > uwzględniających sprzężenie pomiędzy stanami różnych multipletów. Określenie wartości składowej orbitalnej i spinowej momentu magnetycznego jonu paramagnetycznego o strukturze elektronowej obliczanej w reprezentacji |L,L_z,S,S_z> sprowadza się do prostej interpretacji wartości oczekiwanych L i S.

Zewnętrzne pole magnetyczne znosi degenerację, zmienia wartości energii stanów i miesza funkcje falowe stanów (efekt Zeemana). Znoszenie degeneracji i temperaturowo-zależne obsadzenie stanów prowadzi do formowania zależnego od temperatury momentu magnetycznego jonu. Namagnesowanie M obliczamy jako statystyczną sumę momentów poszczególnych jonów m.

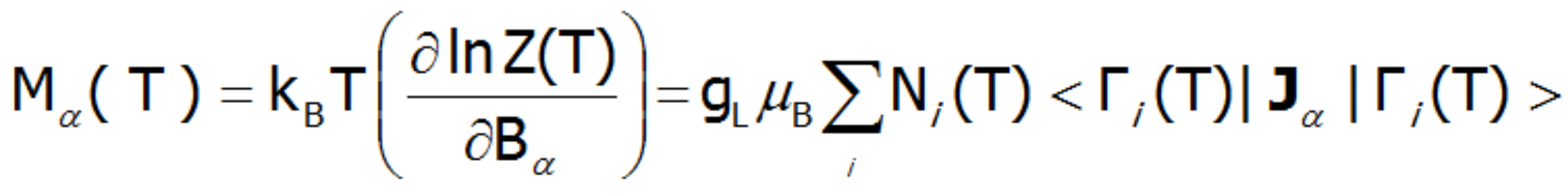
gdzie:
α= x, y, z.
μ_B– Magneton Bohra:

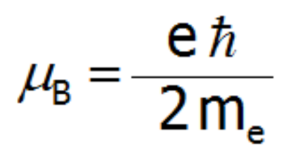
g_J= czynnik Landego
k_B= 1,38 · 10 ^-23 J/K (stała Boltzmanna)

PODATNOŚĆ MAGNETYCZNA
Podatność magnetyczna dla stanu paramagnetycznego obliczana jest zgodnie ze swoją definicją jako stosunek indukowanego namagnesowania do przyłożonego pola magnetycznego. Biorąc pod uwagę związki pomiędzy funkcjami termodynamicznymi, w stosunkowo prosty sposób można obliczyć kierunkowe składowe temperaturowej zależności podatności magnetycznej silnie skorelowanego układu niezamkniętej powłoki elektronowej w strukturze krystalicznej. W granicy niskich pól zewnętrznych podatność definiuje się jako pochodną:

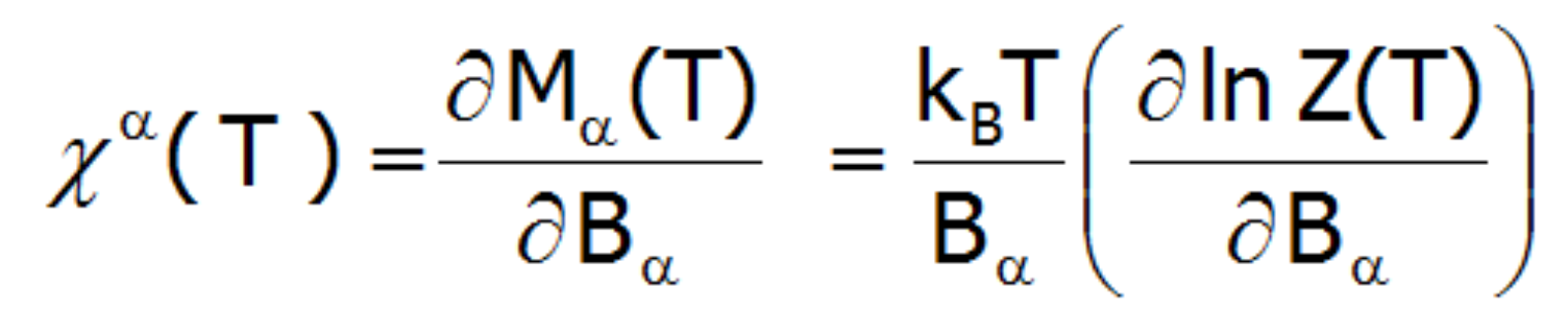
Gdzie index -α jest kierunkiem w lokalnym układzie współrzędnych związanym z osiami kwantyzacji powłoki w polu krystalicznym o określonej symetrii. Biorąc pod uwagę związki opisane w temacie TERMODYNAMIKA UKŁADÓW WIELOELEKTRONOWYCH, elementy macierzowe pomiędzy różnymi stanami otrzymuje się w granicy małych pól: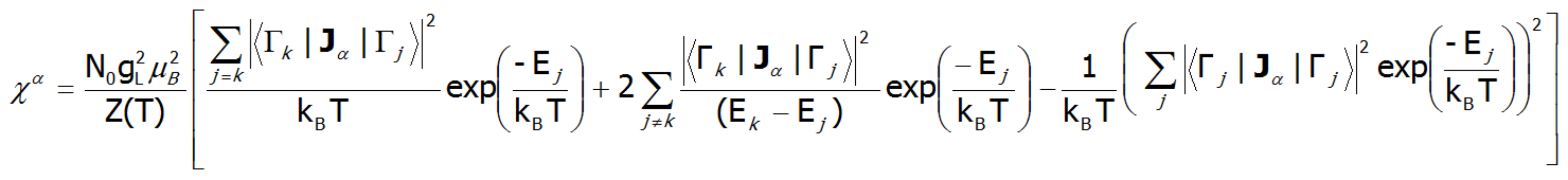

gdzie j, k numeruje stany własne hamiltonianu. Wyrażenie to dla wysokich temperatur, oraz dla bardzo słabych pól krystalicznych redukuje się do podatności typu prawa Curie. W temperaturach porównywalnych z wielkością rozszczepienia stanów pola krystalicznego krzywe podatności tej mogą znacząco odbiegać od kształtu hiperboli. W przypadku pól krystalicznych o niskiej symetrii podatność magnetyczna będzie wykazywać znaczną anizotropię. W strukturze kubicznej χ_x(T)= χ_y(T)= χ_z(T). Podatność magnetyczną można obliczać dla dowolnych pól zewnętrznych jako stosunek namagnesowania traktowanego jako suma indukowanych momentów magnetycznych, do przyłożonego pola. Z uwagi na często obserwowany nieliniowy wzrost wartości momentu magnetycznego, podatności obliczane dla różnych pól mogą się istotnie różnić.

SPEKTROSKOPOWA OBSERWOWALNOŚĆ PRZEJŚĆ MIĘDZYSTANOWYCH
Subtelna struktura elektronowa jest obserwowana w szeregu metod spektroskopowych (ESR EPR, IR spectroscopy, Raman scattering itp.). Obecnie najlepsze metody badania subtelnej struktury elektronowej umożliwia spektroskopia nieelastycznego rozpraszania neutronów INS (Inelastic Neutron Scattering). Dla układu N identycznych jonów przyjmuje się różniczkowy przekrój czynny w eksperymentach INS jako: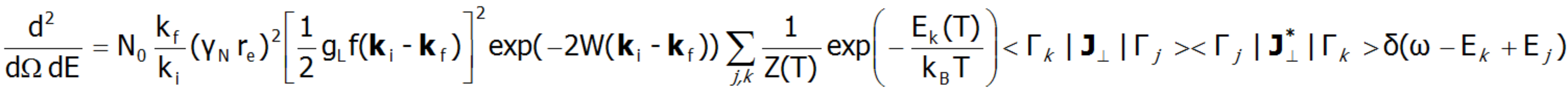

W powyższym równaniu γ_N oznacza czynnik żyromagnetyczny neutronu, r_e jest klasycznym promieniem elektronu r_e=e²/(m_ec²)=2.818·10^-15m, k_i i k_f oznaczają odpowiednio wektor falowy padającego i odbitego neutronu a wyrażenie exp(-2W(k_i-k_f)) reprezentuje czynnik Debye’a-Wallera opisujący termiczne wzbudzanie drgań atomów. Funkcja delta δ (ω - E_j + E_k) odpowiada nieskończenie wąskim stanom pola krystalicznego i często jest zastępowana w dokładnych obliczeniach rozkładem Lorentza z zadanymi szerokościami połówkowymi stanów CEF. Kwadrat elementów macierzowych z powyższego równania, symbolicznie oznaczany jako <Γ_k|J_┴|Γ_j>² w przypadku materiału polikrystalicznego dla dipolowych przejść zastępowany jest przez [²⁰]:

W przypadku monokryształu intensywność rozpraszania neutronów dla przejść dipolowych pomiędzy stanami CEF (Γ_j i Γ_k) przedstawia równanie: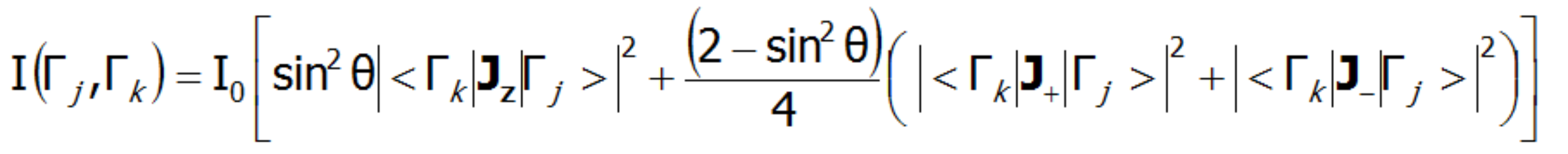

gdzie θ jest kątem pomiędzy wiązką neutronów a osią kwantyzacji z. INS jest bardzo silnym narzędziem pozwalającym na doświadczalną weryfikację teoretycznie obliczonej subtelnej struktury stanów elektronowych. Należy jednak pamiętać, że nie wszystkie stany CEF są widoczne tą techniką - widoczne są tylko te przejścia pomiędzy stanami, gdzie:|<Γ_k|J_z|Γ_j>|, |<Γ_k|J_-|Γ_j>|, |<Γ_k|J₊|Γ_j >| nie jest zerowe.