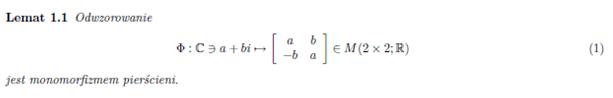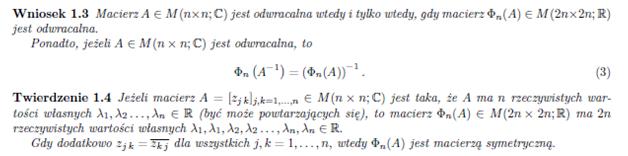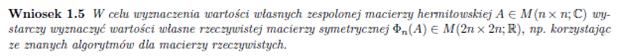TEORIA

OBLICZENIA MACIERZOWE
Obliczenia właściwości magnetycznych rzeczywistych materiałów krystalicznych, zawierających jony metali o niezamkniętej powłoce elektronowej: 2p, 3p, 3d, 4d,5d, 4f  i 5f  wymagają pracy z macierzami znacznego rzędu a w szczególności z macierzami zawierającymi wyrazy zespolone. Główne obliczenia na macierzach opierają się na diagonalizacji macierzy hamiltonianu oddziaływań. W przypadku obliczeń stosowanych w aplikacji ATOMIC MATTES -jest to metoda diagonalizacji  Jacobiego, specjalnie dostosowana do konkretnej sytuacji obliczania zespolonych hamiltonianów CEF i oddziaływań magnetycznych.

DIAGONALIZACJA JACOBIEGO
Metoda Jacobiego jest metodą iteracyjną, służącą do rozwiązywania pełnego zagadnienia własnego rzeczywistych macierzy symetrycznych. W metodzie Jacobiego macierz A przekształcana jest przez podobieństwo ciągiem obrotów. Są one dobrane w ten sposób, że konstruowane macierze A_k (A₁ = A) dążą do  D = diag (λ_i ).

W klasycznym wariancie metody w jej k – tym kroku wyszukuje się największy co do modułu pozadiagonalny element macierzy  A_k = (a_ij) – przyjmijmy, że jest nim  a_pq. Następnie  A_k  przekształcana jest przez ortogonalne podobieństwo obrotem  T_pq.  Macierz transformacji  T_pq  różni się od jednostkowej tylko elementami  t_pp = t_qq = cosθ  i  t_pq =  - t_qp = sinθ .  Kąt obrotu θ określamy tak, aby wyzerować właśnie największy pozadiagonalny element, tzn. a_pq.  Konstruujemy zatem kolejną macierz:

Jest ona symetryczna i różni się od A_k  jedynie elementami w kolumnach i wierszach o numerach p i q. Z warunku, że elementem  A_k+1  o indeksie (p, q) ma być zero otrzymujemy zależność:

Z tej zależności łatwo już znaleźć kąt θ  i dokonywać dalszych przekształceń.

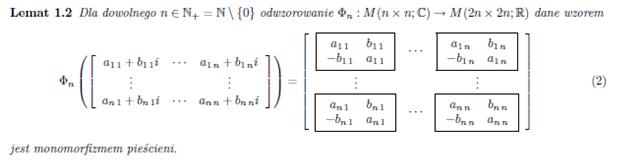
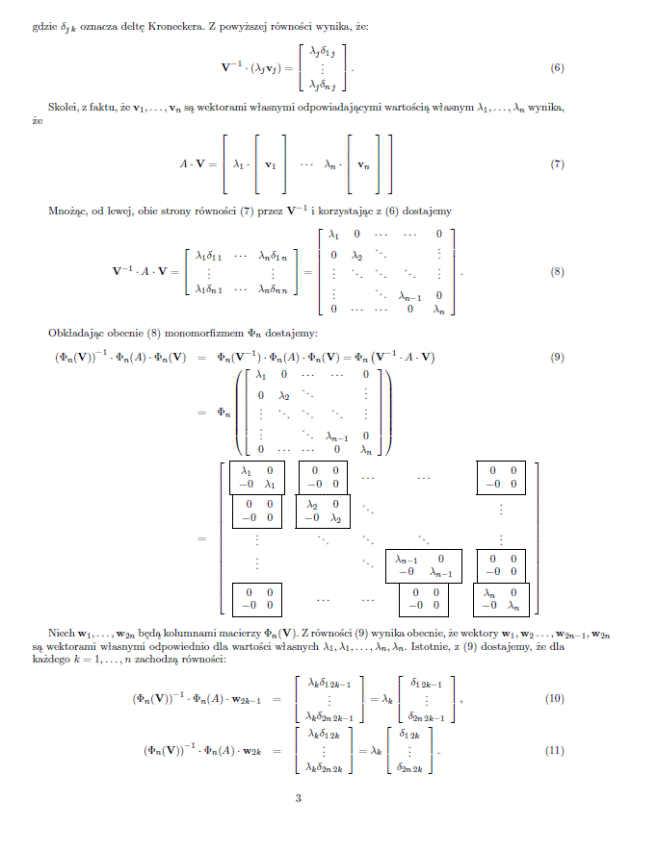
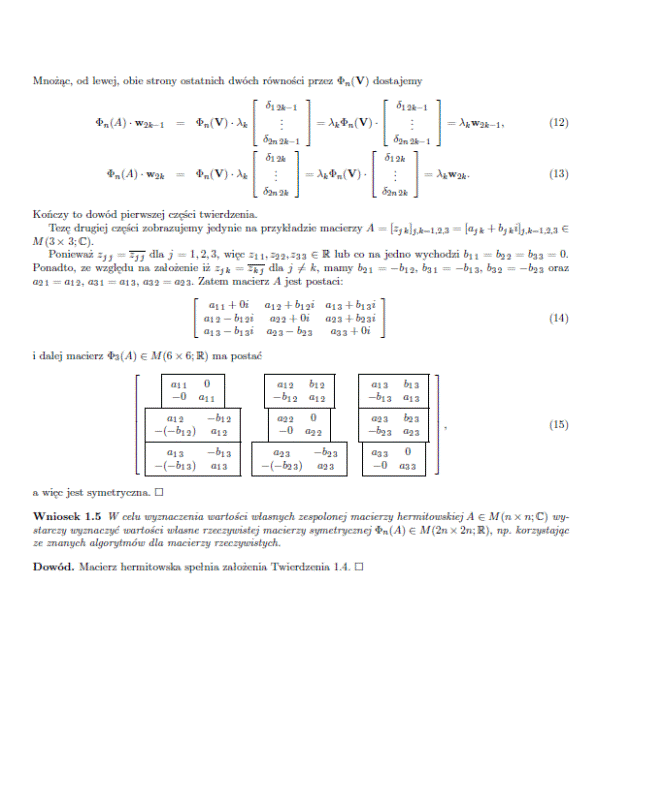
Metoda Jacobiego jest początkowo zbieżna liniowo. Po wykonaniu dużej liczby kroków zbieżność staje się w przybliżeniu kwadratowa. Dokładne obliczenia macierzowe, biorące pod uwagę wszystkie 3 kierunki (x, y, z), wymagają zastosowania macierzy zespolonych. Teoria umożliwiająca przekształcenia i obliczenia z takimi macierzami została opracowana przez  pana dr hab. Marka Karasia i przewiduje rozwinięcie macierzy n x n wymiarowych na 2n x 2n wymiarowe według poniższych lematów: